Angles in triangles worksheet answers – Welcome to the definitive guide on angles in triangles! This comprehensive worksheet will equip you with the knowledge and understanding to conquer any triangle-related problem. Dive in and master the intricacies of triangle angles with confidence.
Within these pages, you’ll explore the Triangle Sum Theorem and Exterior Angle Theorem, unravel the mysteries of different triangle types, and delve into the fascinating world of angle bisectors. Prepare to uncover the secrets of angle relationships and angle measurement techniques.
The journey begins now!
Triangle Angle Theorems

Triangle angle theorems provide relationships between the angles of a triangle. These theorems are fundamental in geometry and are used to solve various problems involving triangles.
Triangle Sum Theorem
The Triangle Sum Theorem states that the sum of the interior angles of a triangle is always 180 degrees. This theorem is a fundamental property of triangles and is often used to find the measure of an unknown angle.
Formula:A + B + C = 180°
Exterior Angle Theorem
The Exterior Angle Theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two opposite interior angles. This theorem is used to find the measure of an unknown exterior angle.
Formula:∠BAC = ∠ABC + ∠BCA
Examples
- Example 1:Find the measure of angle C in a triangle with angles A = 60° and B = 70°.
- Using the Triangle Sum Theorem, we have:
A + B + C = 180°
60° + 70° + C = 180° C = 180° – 60° – 70° C = 50°
- Using the Triangle Sum Theorem, we have:
- Example 2:Find the measure of the exterior angle at vertex A in a triangle with angles B = 40° and C = 50°.
- Using the Exterior Angle Theorem, we have:
∠BAC = ∠ABC + ∠BCA
∠BAC = 40° + 50° ∠BAC = 90°
- Using the Exterior Angle Theorem, we have:
Types of Triangles
Triangles can be classified into different types based on the measures of their angles. This classification helps us understand their properties and applications in various fields.
The three main types of triangles based on angle measures are:
Acute Triangle
- An acute triangle has all three interior angles less than 90 degrees.
- The sum of the interior angles of an acute triangle is always 180 degrees.
Right Triangle
- A right triangle has one interior angle measuring exactly 90 degrees.
- The other two interior angles are both acute, and their sum is 90 degrees.
- The side opposite the right angle is called the hypotenuse, and it is always the longest side.
Obtuse Triangle, Angles in triangles worksheet answers
- An obtuse triangle has one interior angle greater than 90 degrees.
- The other two interior angles are both acute, and their sum is less than 90 degrees.
| Type of Triangle | Interior Angles | Sum of Interior Angles |
|---|---|---|
| Acute Triangle | All angles less than 90 degrees | 180 degrees |
| Right Triangle | One angle 90 degrees, two angles less than 90 degrees | 180 degrees |
| Obtuse Triangle | One angle greater than 90 degrees, two angles less than 90 degrees | Less than 180 degrees |
Real-World Applications of Different Triangle Types
The different types of triangles have various applications in real-world scenarios, including:
- Acute triangles:Used in architecture (e.g., roof trusses), engineering (e.g., bridges), and design (e.g., logos).
- Right triangles:Fundamental in trigonometry, used in surveying, navigation, and construction.
- Obtuse triangles:Found in nature (e.g., leaf shapes), used in architecture (e.g., vaulted ceilings), and design (e.g., artwork).
Angle Bisectors
In geometry, an angle bisector is a ray that divides an angle into two equal angles.
To construct an angle bisector using a compass and straightedge, follow these steps:
- Draw the angle.
- Place the compass point on the vertex of the angle.
- Draw an arc that intersects both sides of the angle.
- Without changing the compass width, place the compass point on one of the intersections of the arc and the sides of the angle.
- Draw another arc that intersects both sides of the angle.
- The intersection of the two arcs is the point on the angle bisector.
- Draw a ray from the vertex of the angle through the point on the angle bisector.
Properties of Angle Bisectors
- An angle bisector divides the angle into two equal angles.
- An angle bisector is perpendicular to the line segment connecting the two sides of the angle.
- The angle bisector of an equilateral triangle is also the median and altitude of the triangle.
- The angle bisector of a right triangle is also the median and altitude of the triangle.
Angle Relationships
Angle relationships describe the interactions between angles formed when lines intersect or are parallel. Understanding these relationships is essential for solving geometry problems involving angles.
Parallel Lines and Transversals
When a transversal intersects two parallel lines, it creates eight angles. These angles have specific relationships that can be used to solve problems.
- Corresponding Angles:Angles that are in the same position relative to the parallel lines and the transversal are congruent. (e.g., ∠1 and ∠5, ∠2 and ∠6)
- Alternate Interior Angles:Angles that are on opposite sides of the transversal and inside the parallel lines are congruent. (e.g., ∠3 and ∠5, ∠4 and ∠6)
- Alternate Exterior Angles:Angles that are on opposite sides of the transversal and outside the parallel lines are congruent. (e.g., ∠1 and ∠7, ∠2 and ∠8)
These angle relationships can be used to find unknown angles in a diagram involving parallel lines and a transversal.
Angle Measurement
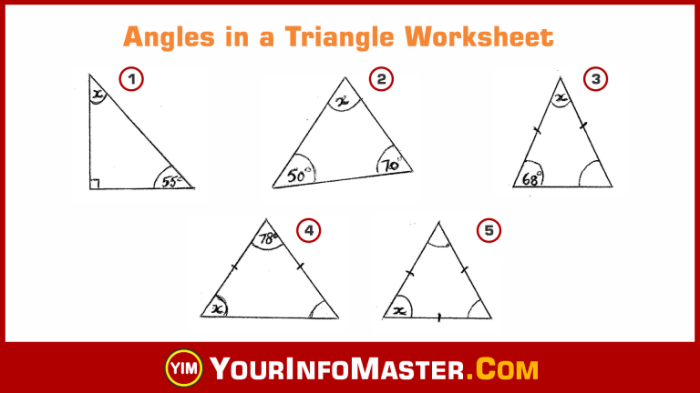
Angle measurement is the process of determining the size of an angle. Angles are measured in degrees, minutes, and seconds, with 360 degrees in a full circle.
Using a Protractor
A protractor is a tool used to measure angles. It is a semicircular device with a scale marked in degrees. To use a protractor, place the center of the protractor on the vertex of the angle and align the 0-degree mark with one side of the angle.
Then, read the angle measure where the other side of the angle intersects the protractor scale.
Solving Problems with Angle Measures
Angle measures can be used to solve a variety of problems, such as finding the sum or difference of angles, determining the measure of an unknown angle, and constructing angles with specific measures.
Example:
Find the measure of the missing angle in the triangle below.
The sum of the angles in a triangle is 180 degrees. So, the missing angle is 180- 60 – 45 = 75 degrees.
FAQ Explained: Angles In Triangles Worksheet Answers
What is the Triangle Sum Theorem?
The Triangle Sum Theorem states that the sum of the interior angles of a triangle is always 180 degrees.
How do I find the measure of an exterior angle?
The measure of an exterior angle is equal to the sum of the measures of the two non-adjacent interior angles.
What are the different types of triangles based on angle measures?
Triangles can be classified as acute (all angles less than 90 degrees), right (one angle is 90 degrees), or obtuse (one angle is greater than 90 degrees).