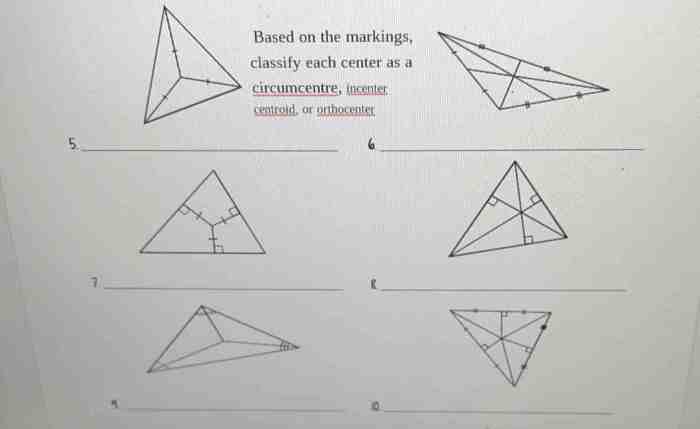
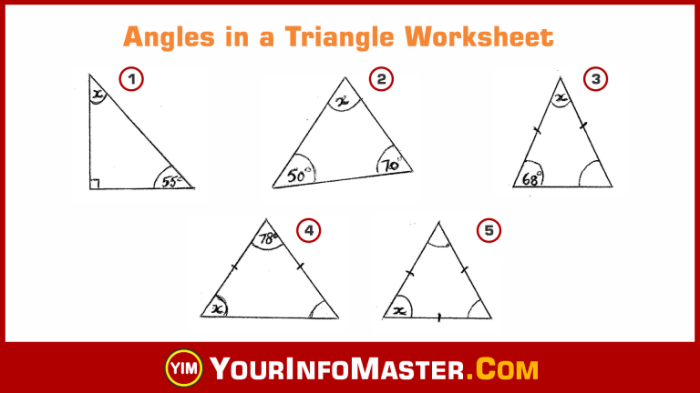
Classify each center as a circumcenter incenter centroid or orthocenter – Classify each center as a circumcenter, incenter, centroid, or orthocenter. This comprehensive guide explores the definitions, geometric relationships, classification methods, applications, and examples of these triangle centers, providing a deeper understanding of their significance in geometry and problem-solving.
Triangle centers, including the circumcenter, incenter, centroid, and orthocenter, play crucial roles in defining the geometry of triangles. By understanding their properties and interrelationships, we gain valuable insights into the behavior and characteristics of triangles, enhancing our geometric reasoning and problem-solving abilities.
Definitions and Characteristics
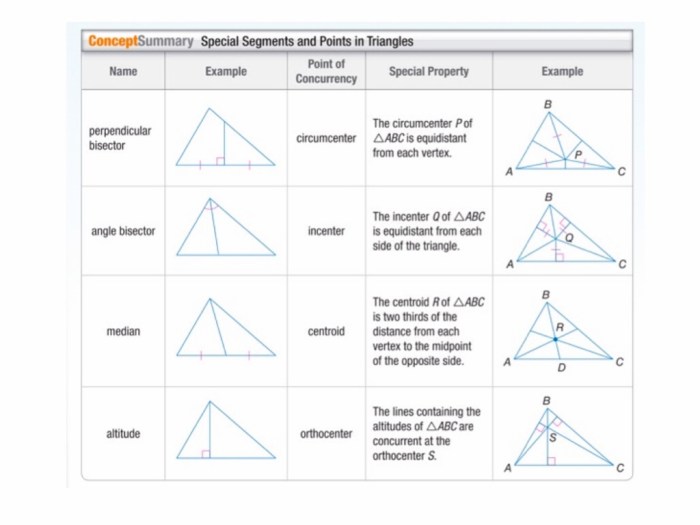
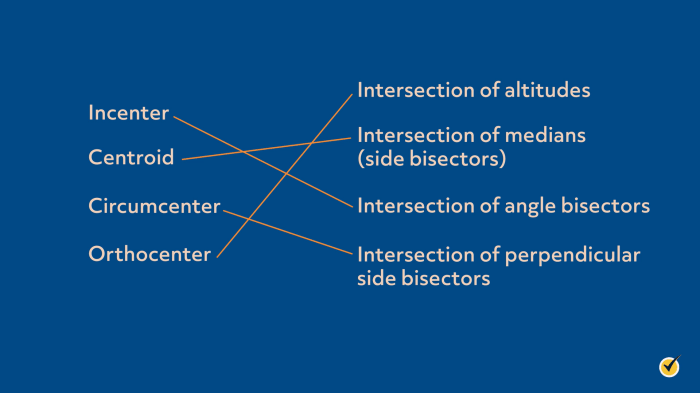
A triangle is a polygon with three sides and three angles. A triangle’s center is a point that is equidistant from all three vertices. There are four main types of triangle centers: the circumcenter, incenter, centroid, and orthocenter.
| Center Type | Definition | Key Characteristics |
|---|---|---|
| Circumcenter | The point where the perpendicular bisectors of the three sides of a triangle intersect | Equidistant from all three vertices |
| Incenter | The point where the angle bisectors of the three angles of a triangle intersect | Equidistant from all three sides |
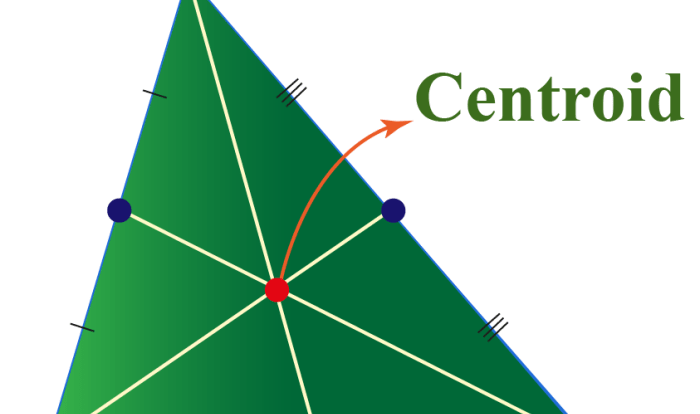
| Centroid | The point where the three medians of a triangle intersect | Divides each median into a 2:1 ratio |
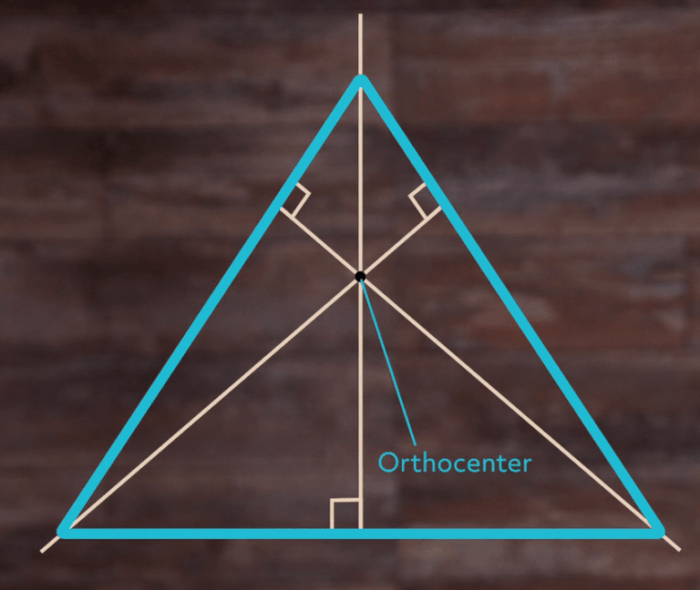
| Orthocenter | The point where the three altitudes of a triangle intersect | The point where the three altitudes of a triangle intersect |
Geometric Relationships, Classify each center as a circumcenter incenter centroid or orthocenter
The circumcenter, incenter, centroid, and orthocenter of a triangle are all related to each other. The circumcenter is the center of the circle that circumscribes the triangle, while the incenter is the center of the circle that is inscribed within the triangle.
The centroid is the point where the three medians of the triangle intersect, and the orthocenter is the point where the three altitudes of the triangle intersect.
The following diagram shows the geometric relationships between the circumcenter, incenter, centroid, and orthocenter of a triangle:
[Diagram of the geometric relationships between the circumcenter, incenter, centroid, and orthocenter of a triangle]
As you can see from the diagram, the circumcenter, incenter, centroid, and orthocenter are all located on the same line. This line is called the Euler line. The Euler line is named after the Swiss mathematician Leonhard Euler, who first discovered the relationship between these four points.
Classification Methods
There are a number of different methods that can be used to classify a triangle center as a circumcenter, incenter, centroid, or orthocenter. One common method is to use the following criteria:
- If the center is equidistant from all three vertices, then it is the circumcenter.
- If the center is equidistant from all three sides, then it is the incenter.
- If the center divides each median into a 2:1 ratio, then it is the centroid.
- If the center is the point where the three altitudes of the triangle intersect, then it is the orthocenter.
Another method for classifying triangle centers is to use a flowchart or decision tree. The following flowchart can be used to classify a triangle center:
[Flowchart or decision tree for classifying triangle centers]
Applications and Examples
Classifying triangle centers has a number of applications in geometry. For example, the circumcenter can be used to find the radius of the circle that circumscribes a triangle. The incenter can be used to find the radius of the circle that is inscribed within a triangle.
The centroid can be used to find the center of gravity of a triangle. And the orthocenter can be used to find the altitude of a triangle.
Here are some examples of problems or scenarios where classifying triangle centers is useful:
- Finding the radius of the circle that circumscribes a triangle
- Finding the radius of the circle that is inscribed within a triangle
- Finding the center of gravity of a triangle
- Finding the altitude of a triangle
- Determining whether a triangle is equilateral, isosceles, or scalene
Understanding triangle centers can enhance geometric reasoning and problem-solving skills. By being able to classify triangle centers, you can gain a deeper understanding of the relationships between the different parts of a triangle.
FAQ Compilation: Classify Each Center As A Circumcenter Incenter Centroid Or Orthocenter
What is the difference between a circumcenter and an incenter?
The circumcenter is the center of the circle that circumscribes the triangle, while the incenter is the center of the circle that is inscribed within the triangle.
How can I determine the centroid of a triangle?
The centroid is the intersection point of the three medians of the triangle, which are the lines connecting the vertices to the midpoints of the opposite sides.
What is the significance of the orthocenter?
The orthocenter is the point where the three altitudes of the triangle intersect. It is also the center of the circle that passes through the vertices of the triangle.